cl Archives - Jim Dougherty

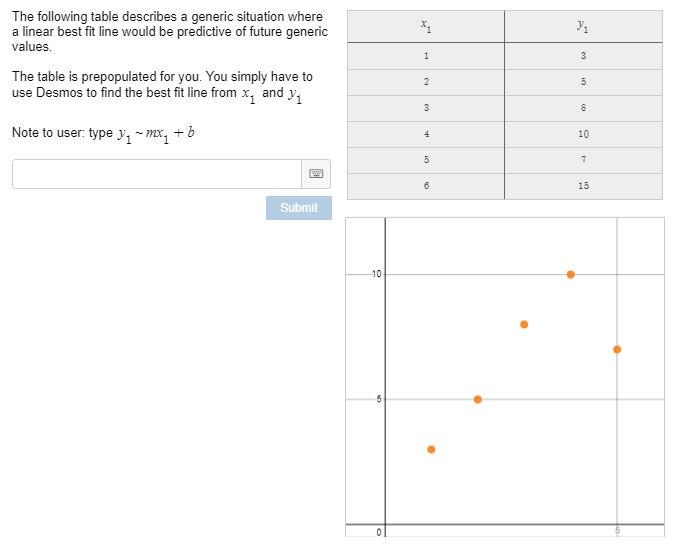
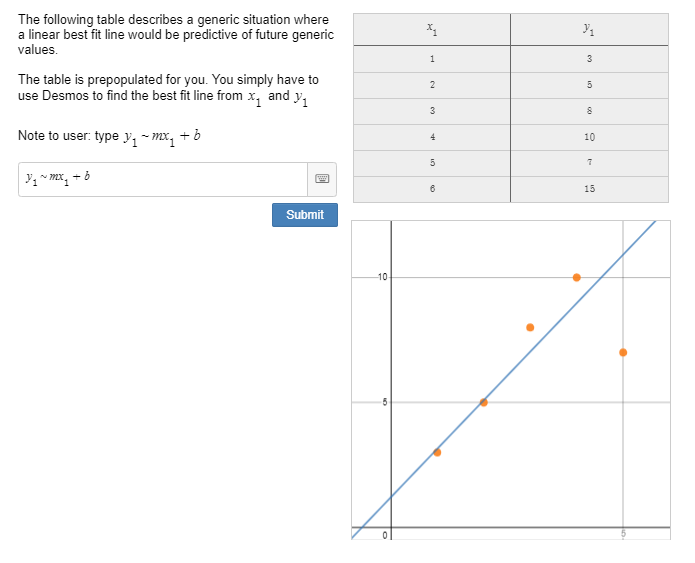
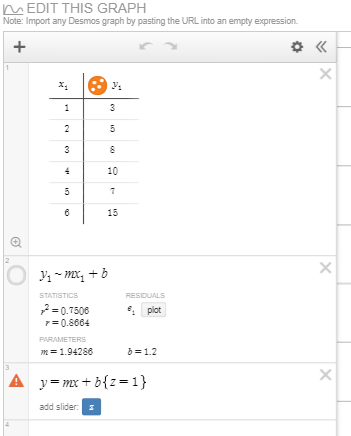
The Desmos Computation Layer (CL) gives you a multitude of ways to offer students real-time feedback when they are completing problems in an activity. In this post, I’ll discuss how to provide immediate feedback to students based on their input in a “Math Input” item, a “Multiple Choice” item, a “Checkboxes” item, and “Ordered List” item, a “Table” item, and a “Card Sort” item.

click this link to see a Desmos activity that demonstrates the code used in this post

Feedback using a “Math Input” item

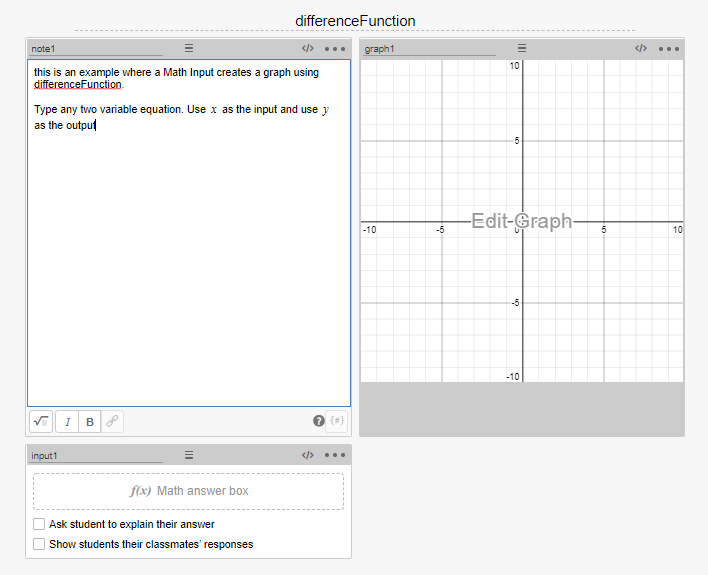
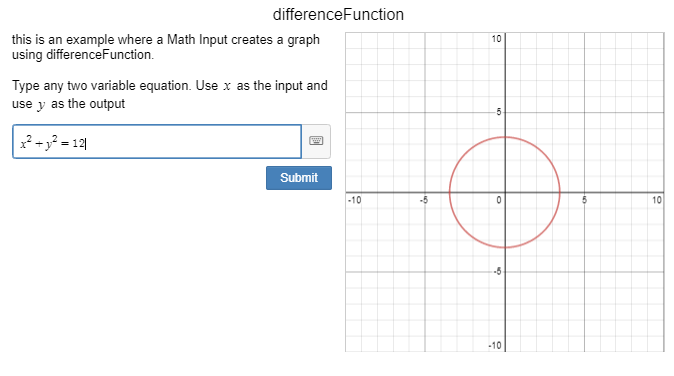
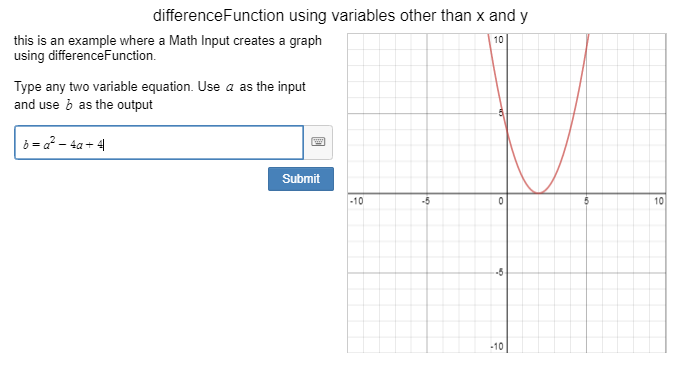
Providing feedback using a “Math Input” item is the easiest way to provide feedback to students in an activity. The way that I favor setting this up is to use two “Note” items and one “Math Input” item. Like this:

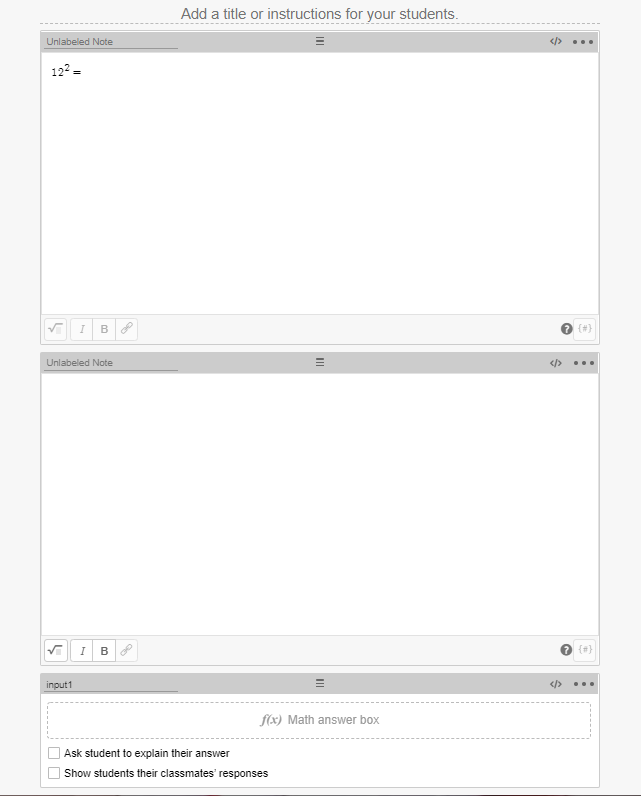
My preference is to put the question / problem in the first “Note” item, and the feedback in the CL of the second “Note” item. The feedback is presented as a “content:” sink. Notice that the “when” conditional statement always has an “otherwise” condition, stating what happens as default if other conditions aren’t met.

In the example problem above, I would write the feedback in the “Note” item 2 CL like this:

content:
when 
input1.numericValue=144
 "? CORRECT!" 
otherwise ""

This code says that whenever the value in the “Math Input” item equals 144, The content of this cell will be “? CORRECT!”, and if the value is not equal to 144, there will be no content.

About emojis: I favor putting emojis in the feedback, but you can write whatever feedback you prefer. In order to add an emoji you can add them to the text of any question or content that you like. In Windows, you can add an emoji by right-clicking your mouse or by using the shortcut Win+Period.

You could also write feedback for both a correct and an incorrect answer. Using the same example from above, a code could be:

content:
when input2.numericValue=144 and input2.submitted "? CORRECT!" 
when not(input2.numericValue=144) and input2.submitted "? Not quite. Remember that an exponent describes how many times to multiply a base."
otherwise ""

In this example, I wrote feedback to the student if the answer isn’t correct. I also added the condition “.submitted” to each condition. The purpose of “.submitted” is so that the coaching feedback doesn’t appear before the student is able to enter their answer completely.

Feedback using a “Multiple Choice” item

The feedback for a “Multiple Choice” item in the CL is very similar to a “Math Input” item. I like to ask the question in “Note” item 1, write the CL feedback in “Note” item 2, and the student input is a “Multiple Choice” item. Like this:

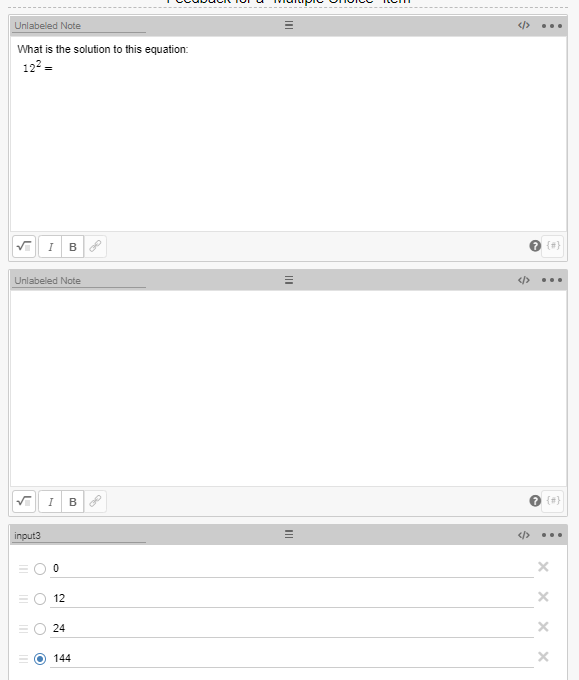
The correct answer for the “Multiple Choice” item would be the fourth answer, so an example of feedback in the “Note” item CL would be:

content: 
when input3.isSelected(4) "? CORRECT!" 
otherwise ""

This code describes that when the fourth choice is chosen, a student would receive feedback that the item is correct.

Feedback using a “Checkboxes” item

“Checkboxes” items require a little more work than other CL input types. The reason for this is that you have to identify both conditions of each answer in order to give proper feedback. We do this by identifying incorrect answers with the not( ) condition. Here’s the setup:

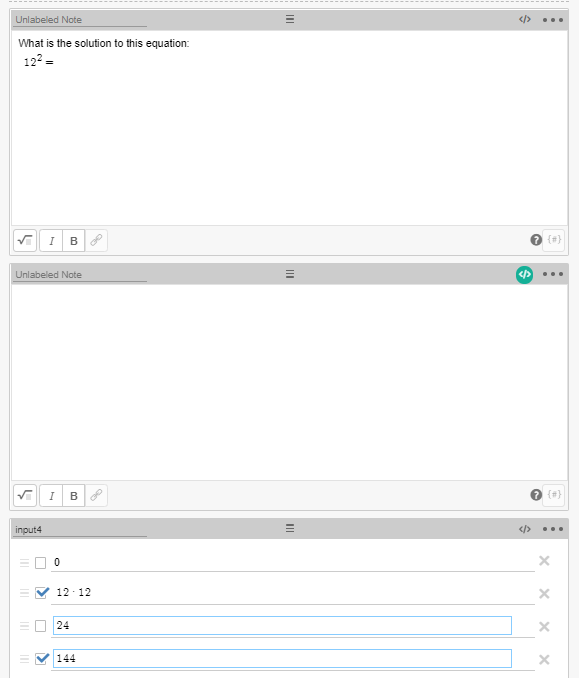
You can see from this problem that answers 2 and 4 are correct, and that answers 1 and 3 are incorrect. A code to provide feedback for this would have to address the condition for every checkbox, for example:

content: 
when 
not(input4.isSelected(1)) and
input4.isSelected(2) and
not(input4.isSelected(3)) and
input4.isSelected(4) "? CORRECT!" 
otherwise ""

An alternative to just providing one correct answer for a “Checkboxes” would be to provide feedback for all answers (or as many as you would find appropriate). The upside to this would be that students get immediate feedback for each answer, but the downside would be this would make answering the question rather simple.

There are probably other strategies for doing this, but my basic setup for providing feedback for each entry would be to create variables for each answer, in this case a, b, c, and d. The “content:” sink would then just present feedback for every box that the students check. An example of code for this would be:

a= when input5.isSelected(1) "? Oh no! #1 is not correct." otherwise ""
b= when input5.isSelected(2) "Number 2 is ?" otherwise ""
c= when input5.isSelected(3) "? Oh no! #3 is not correct." otherwise ""
d= when input5.isSelected(4) "Number 4 is ?" otherwise ""
content:
"${a}
${b}
${c}
${d}"

A note: putting a variable or an input into ${ } in the CL will present the text of that input or variable as written.

Feedback using an “Ordered List” item

Ordered lists are pretty easy to give binary feedback for, as long as you choose the option in the “Ordered List” item to “Use Order as Answer Key.”

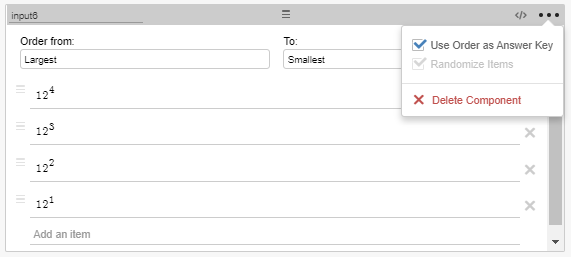
When an ordered list is set up like this, we can use “.matchesKey” in the CL to give feedback for the correct order. Here is an example:

content:
when
input6.matchesKey "? CORRECT!" otherwise ""

If for some reason you don’t choose “Use Order as Answer Key,” you can still provide feedback (and identify the correct answer) using “.orderAtIndex” Here is an example of the “orderedList”:

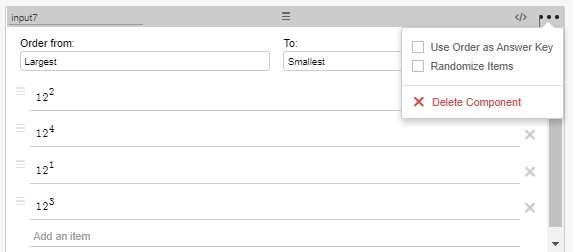
The correct answer for this example would be 2, 4, 1, 3. This would be an example of using “.orderAtIndex” to give feedback when correct:

content:
when
input7.itemAtIndex(1)=2 and
input7.itemAtIndex(2)=4 and
input7.itemAtIndex(3)=1 and
input7.itemAtIndex(4)=3
"? CORRECT!" otherwise ""

Feedback using a “Table” item

There are a few ways that you can program feedback for a table. The way that I prefer is to create an additional table and to program feedback into each line. Here’s a basic setup with a “Note” item to describe the problem and a “Table” item. Notice the third column with the emoji is the feedback column:

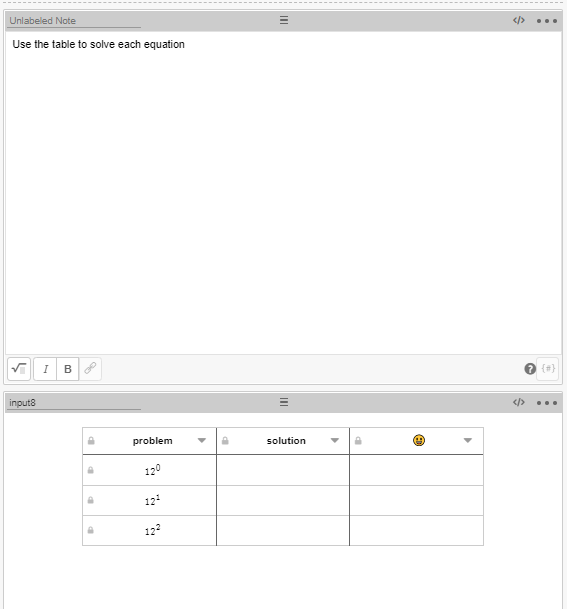
Emoji / table note: If you want to program emojis into a table, you need to format that column as text. If the column is set up to read latex, your emojis will not show up. You can change this in the column drop-down:

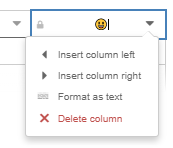
In this example, I’m going to use the “cellContent:” sink to populate the third column in the CL for the table. This is different from the other methods in that the code is written in the input item and not in a different note. Here’s an example of code that you can use to do this:

cellContent(1,3):
when input8.cellNumericValue(1,2)=1 "✔" otherwise ""
cellContent(2,3):
when input8.cellNumericValue(2,2)=12 "✔" otherwise ""
cellContent(3,3):
when input8.cellNumericValue(3,2)=144 "✔" otherwise ""

This code identifies the target cell (row,column) and then sets the condition for the emoji check feedback to appear. When a student completes the table it will look like this:

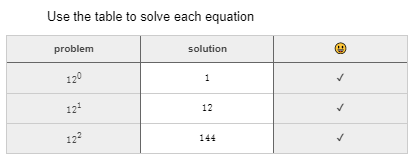
Alternatively, you could create another “Note” item and program feedback for each line as conditional variables. An example of this code would look like this:

a= when input8.cellNumericValue(1,2)=1 "? Equation 1 is CORRECT!" otherwise ""
b= when input8.cellNumericValue(2,2)=12 "? Equation 2 is CORRECT!" otherwise ""
c= when input8.cellNumericValue(3,2)=144 "? Equation 3 is CORRECT!" otherwise ""
content:
"${a}
${b}
${c}"

Feedback using a “Card Sort” item

The last type of item we’ll talk about is the “Card Sort” item. This is a little different than the others because you cannot add a note a card sort. In this case, we’ll program feedback into the “subtitle:” Here’s the basic setup:

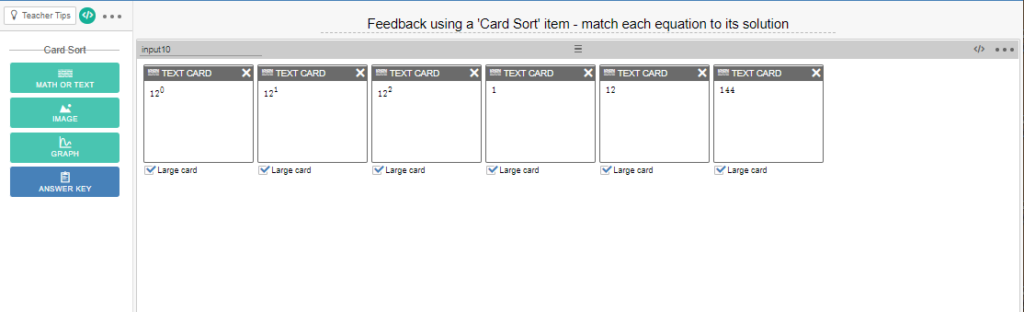
An important aspect to make this work is that you must go into the “Answer Key” and define the correct answers in order to give feedback. An example of this is here:

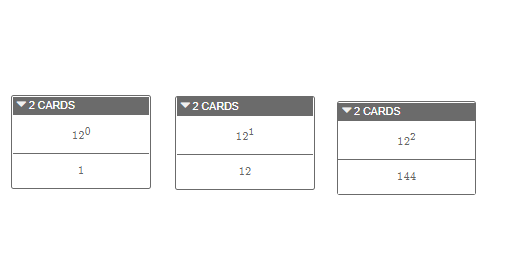
After defining the answer key, you will go into the CL (this is located in the left hand corner of the screen beneath the dashboard and to the right of “Teacher Tips”). In the CL, you’ll use the “subtitle:” sink to provide feedback. In this example, I defined variables to give feedback as students get pairs correct:

subtitle: "You have ${a} answers correct"
a=
when input10.totalCorrectCards=2 "one"
when input10.totalCorrectCards=4 "two"
when input10.totalCorrectCards=6 "all"
otherwise "no"

Because these cards are correct in pairs, I use “.totalCorrectCards” to define that a student receives feedback for every set of pairs that they find. A student would see a screen like this:

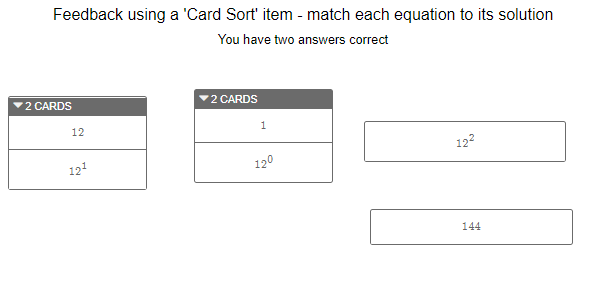
If you wanted to only provide feedback when all of the solutions are correct, you could use “.matchesKey” to only give feedback when all are correct. An example of this code would be:

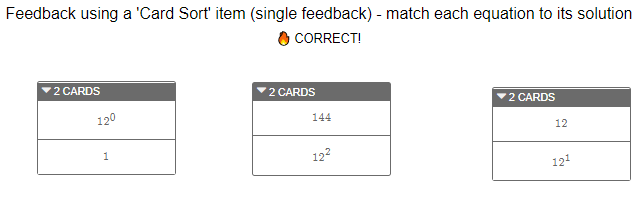
subtitle: when input11.matchesKey "? CORRECT!" otherwise ""

In this situation, the student would only see feedback if they match all of the cards correctly. Students would see a screen like this:

And that’s all that I have for now. If there’s a situation I didn’t demonstrate leave me a message in the comments and I will try to add it.

click this link to see a Desmos activity that demonstrates the code used in this post

One of the coolest ways to utilize Desmos in the computation layer (CL) is to be able to visualize student answers on the graph. I’m going to show two approaches to this: a direct approach, and indirect approach.

the direct approach

The most straightforward situation that you would use this feature would be for a student to enter an equation in a “Math Input” box and for it appear on a graph. The general setup would involve a “Note,” a ‘Math Input,” and a “Graph” box like this:

To do this, you’ll go to the graph CL and use the differenceFunction to evaluate the equation. differenceFunction subtracts the left side of the typed equation from the right side of the typed equation. The code in this example would look like this:

function("f"): parseEquation(input1.latex).differenceFunction("x","y")

This defines a function f that subtracts the left side of the input1 equation from the right side of the input1 equation.

The next step would be to click into graph1 itself and type the following code in the first line of the graph (just as if you were doing it in the graphing calculator):

0=f(x,y)

Because f is a function that subtracts the left side of input1 from the right side, this graphs all of the points where the equation is true. Now any equation that you type into the Math Input will be shown on the graph.

using variables other than x and y

The Desmos graphing calculator is pretty finicky when it comes to variables, but you can create graphing activities using variables other than x and y using the same general setup.

For the code that we put in the graphing later CL, instead of defining the variables in the differenceFunction as “x” and “y”, you would define these as other variables. For example, if you wanted to use a and b as an alternative, you would type:

function("f"): parseEquation(input2.latex).differenceFunction("a","b")

This defines a as your output variable and b as your input variable. Counterintuitively, the input in the actual graph will stay the same:

0=f(x,y)

Once you’ve entered those two lines into your graph, you can type equations with new variables and it will interpret them as the input and output in your graph:

a workaround if parseEquation won’t do

One workaround that I’ve used in certain circumstances is to ignore trying to translate a computation to the graph. Instead, if an input is correct I will use a “number:” defined in the graph CL to trigger the correct graph.

I use this frequently with statistics to show a best fit line. Rather than having students spend their time populating a table in the Desmos calculator and trying to find the line of best fit, I will prepopulate the graph in the graph and make the best fit line only appear conditionally when they type the correct equation in the input.

To set this up, I define a number in the graph CL:

number("z"): when input3.latex="y_{1}\sim mx_{1}+b" 1 otherwise 0

This defines a number z that is equal to 0 unless the correct Latex is entered (note: using Latex for correct answers is generally a poor idea since it must be typed as an exact match – although in this circumstance it has been pretty successful).

Then, in the actual graph, I create the table, find the best fit line, and then restrict the best fit line to show only if the number z is equal to 1. Like this:

This is a workaround to use sparingly, but in the right situation may be useful. When I’m stuck, sometimes I find it useful to give students the appearance that a computation is being made while also saving me the trouble of trying to code something beyond my capability.

caution: don’t use rawExpression

A last word of caution about the deprecated feature: rawExpression. There are a few posts in the CL support forum that recommend using the rawExpression function to graph inputs (rawExpression translates an input directly as typed into the graphing layer). This is super easy to use and was allegedly a little wonky causing Desmos to deprecate the function.

Why shouldn’t you use it? Because it was deprecated any activity that uses that command cannot be copied (which is important if you’re sharing your activities with others). I say this from personal experience as I am still rewriting activities from when I didn’t know better.

How to program feedback into a Desmos activity